İlköğretimde Problem Çözme Öğretimi

Yrd.Doç.Dr. Murat ALTUN (*)

GİRİŞ

Bu makalede problem ve problem çözmenin ne olduğu tanıtılmış daha sonra problem türlerinin ve problem çözmenin doğası üzerinde durulmuştur.

Problem ve Problem Çözme:

Problem deyince, çoğunlukla ilkokul matematik ders kitaplarından elde edilen bir anlayışla konu sonlarında verilen dört işleme dayalı matematik problemleri akla gelmektedir (1). “Aralarında 140 km mesafe olan iki bisikletli karşılıklı yola çıkıyorlar. Birincinin saatteki hızı 15 km dir ve iki bisikletli 5 saat sonra karşılaştıklarına göre ikinci bisikletlinin satteki hızı kaç km dir?” örneğinde olduğu gibi. Problem kavramı burada sözü edilenden daha geniş bir anlama sahiptir ve problemin matematikle ilgili olması şart değildir.

Problem kavramıyla ilgili verilen bir tanım şöyledir.

Problem zor ya da sonucu belirsiz bir sorudur. Çözümü bir araştırma veya tartışma gerektirir. Kişi çözümü bulma konusunda hazırlıksız fakat isteklidir (2)

Bu tanım problemin üç temel özelliğini ortaya koymaktadır. Bunlar (1) Problemin karşılaşan kişi için bir güçlük olduğu, (2) kişinin onu çözmeye ihtiyaç duyduğu ve (3) kişinin bu problemle daha önce karşılaşmamış olduğu, çözümle ilgili bir hazırlığının bulunmadığıdır. Bu özellikle problem kavramıyla ilgili bazı sınırlamalar getirmektedir. Bunlar, birkez karşılaşılıp çözüldükten sonra aynı durumun problem olmadığı, bazı kişiler için problem olan bir durumun diğer bazılarına göre olmadığı, çözümün aniden ortaya çıkmadığı ve bir çaba gerektirdiğidir.

Problem çözme ise problem kavramına bağlı olarak “Ne yapılacağının bilinmediği durumlarda yapılacak olanı bilmektir” şeklinde tanımlanabilir. Bir problemle karşılaşıldığı zaman onun anlaşılması çok önemlidir. Birey anlayamadığı bir problem için, çözüm öneremez, herhangi bir strateji tespit edip bunu uygulamaya koyamaz. Bu açıklamalara göre problem çözme süreci; “Net olarak tasarlanan fakat hemen ulaşılamayan bir hedefe varmak için kontrollü etkinliklerle araştırma yapmadır” şeklinde açıklanabilir.

Problemlerin Sınıflandırılması

Problemlerin değişik yaklaşımlarla sınıflandırılmaları yapılabilir. Öğretimindeki amaçlar esas alınarak problemler iki sınıfa ayrılabilir. Rutin ve rutin olmayan problemler.

Rutin (Dört İşlem) Problemler: Bunlar matematik ders kitaplarında çokça yer alan ve dört işlem problemleri olarak bilinen problemlerdir. Yabancı literatürde word problem ya da story problem olarak adlandırılırlar. Rutin problemler bir ya da çok işlemli olabilirler. “Ali 212 sayfalık bir kitabın birinci gün 30, ikinci gün 42 sayfasını okudu. Üçüncü gün kitabın yarısına geldiğine göre üçüncü gün kaç sayfa okumuştur?” bu türden bir problemdir. Dört işlem problemlerinin öğretiminin amacı, çocukların günlük hayatta çok gerekli olan işlem becerilerini geliştirmeleri, problem hikayesinde geçen bilgileri matematik eşitliklere aktarmayı öğrenmeleri, düşüncelerini şekillerle anlatmaları, yazılı ve görsel yayınları anlamaları ve problem çözmenin gerektirdiği temel becerileri kazanmalarıdır.

Rutin Olmayan (Gerçek) Problemler: Rutin olmayan problemlerin çözümleri işlem becerilerinin ötesinde, verileri organize etme, sınıflandırma, ilişkileri görme gibi becerilere sahip olmayı ve bir takım aktiviteleri arka arkaya yapmayı gerektirir (3). Örneğin; “Bir adam bir oyundan bir tilki, bir ördek ve bir çuval mısır kazanıyor. Bunlarla birlikte bir nehrin bir kıyısından öbür kıyısına geçmek zorunda fakat, bir kayık var ve çok küçük. Adamla birlikte bu kayık ancak birini alabiliyor. Mısırı geçirse tilki ördeği yiyebilir, tilkiyi geçirse ördek mısırı. Hiçbir zayiyat olmadan bunları karşıya nasıl geçirebilir?” sorusu bu türden bir problemdir. Bu problemler ya gerçek hayatta karşılaşılmış ya da karşılaşılabilecek bir durumun ifadesidirler. Bundan ötürü bunlara gerçek hayat problemleri de denir.

Matematik, fizik ve diğer bazı derslerde üzerinde çalışılan formüllerin ve genellemelerin herbiri de bir gerçek hayat problemi olarak ele alınabilir. 1’den itibaren n tane tek sayının toplamı n2 dir. Üçgenin alanı A=1/2 a. h dir. Serbest düşen bir cismin aldığı yol l=2 gt2 dir gibi. Çağdaş bir öğretim, bu genellemelerin veya formüllerin problem çözme yaklaşımı ile ele alınmasını ve öğrencilere buldurulmasını gerektirir. Rutin olmayan problemleri çözmeyi öğrenen öğrenciler sayısal ilişkileri ve sistematik yapılan görme bakımından gelişirler. Verilerden hareket ederek verilmeyen ya da bilinmeyen kısımlar hakkında tasarım ve kestirimde bulunabilirler.

Rutin olmayan problemlerin, çözümlerinin amacı ise problem çözmenin mantığını ve doğasını kavrama, bir problemle karşılaşıldığında uygun stratejiyi seçme, kullanma ve sonuçları yorumlama yeteneklerini geliştirmektir. Bu amaç problem çözme öğretiminin en temel amacıdır.

İnsan ve toplum hayatında, ne zaman ne tür güçlüklerle karşılaşılacağı ya da ne tür ihtiyaçların doğacağı önceden bilinmediği için, çağdaş eğitim kendi kendine güçlüklerin üstesinden gelebilen insanı yetiştirmeyi hedeflemektedir. Bu bakımdan problem çözme öğretimi önemlidir. Eğitim öğretim faaliyetlerinde problem çözme sadece bir matematik konusu olarak ele alınıp sonra terkedilmemeli, bütün eğitimin odak noktası olmasıdır. Yani öğretimde problem çözme yaklaşımı, en temel yaklaşım olarak benimsenmelidir.

Problem Çözmenin Doğası

Hayatta karşılaşılan bir problemin çözümü aşağıdaki döngüye uygun olarak gerçekleşir. Önce problemin matematik ifadesi elde edilmekte daha sonra problemin matematiksel çözümü yapılmakta son olarak bu çözüm gerçek hayat için yorumlanmaktadır.

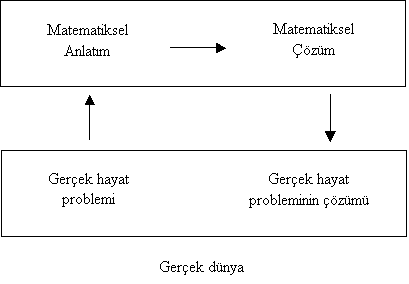
Her gerçek hayat problemi için bu döngü geçerlidir. Bu döngü basit bir problem üzerinde şöyle açıklanabilir (4).

* Gerçek hayat problemi: Öğrenciler pikniğe gidecek. Nasıl?

* Problemin matematiksel anlatımı: Okulun 102 öğrencisi ve 16 kişi taşıyabilecek bir aracı var. Kaç sefer yapmalıdır?

* Matematik problemin çözümü 102:16=6,375

* Gerçek hayat probleminin çözümü: Araç 7 sefer yapmalıdır.

Dört işlem problemlerinin çoğu “matematiksel olarak ifade edilmiş” şekilleriyle verildiklerinden yukarıdaki döngüye tam olarak uymazlar. Döngünün ilk ve son safhası ihmal edilmiş olur.

PROBLEM ÇÖZME ÖĞRETİMİ

Bütün problemlerin çözümünde kullanılan belirli bir yol ya da yöntem yoktur. Eğer böyle bir yöntem olsaydı sorun kökünden halledilirdi.

Çocuklar bir problemle karşılaştıklarında çoğu kez kullanılacak bir kural hatırlamaya çalışırlar. Bu iyi bir girişim değildir. Çünkü problem çözmenin kuralları yok, ancak sistematiği vardır. Öğretmenin temel görevi öğrenciye problem çözmeyle ilgili bu sistematiği ve stratejileri tanıtmak ve bunları kullanabilmeyi öğretmektir.

Rutin olan ve olmayan problemlerin çözümleri konusunda en çok kabul gören süreç George Polya (1887-1985) tarafından verilen dört basamaklı süreçtir. Bu basamakların bilinmesi, problem çözmeyi sağlamaz, ancak problem çözerken bu dört basamağa uygun çalışma biçimi çözümü kolaylaştırır.

Bu basamaklar ve bu basamakların kapsamındaki başlıca etkinlikler şunlardır:

1) Problemin Anlaşılması

(1) Neler verilmiştir?

(2) Neler istemektedir?

Eğer öğrenci bu iki soruya tam olarak cevap verebiliyorsa problemi anlamış demektir. Problemi anlamanın başka göstergeleri de vardır. Öğretmen bunları kullanmak suretiyle öğrencilerin problemi anlayıp anlamadıklarının kontrol edebilir. Bunlar;

(1) Öğrenci problemi vurgu düzeyine uygun okuyabiliyor mu?

(2) Problemde eksik ya da fazla bilgi varmıdır?

(3) Problemden ne tür bilgiler elde edilmektedir?

(4) Problemdeki olaylara ve ilişkilere uygun şekil ya da diyagram çizebiliyor mu?

(5) Problemi parçalara (alt problemlere) ayırabiliyor mu?

2) Çözümle İlgili Stratejinin Seçilmesi

Problem anlaşıdıktan sonra sıra çözümde kullanılacak olan stratejinin seçilmesine gelir. Bu safhada öğretmenin rolü, bazı sorular yönelterek öğrencilerin uygun stratejileri seçmelerini sağlamaktır. Ancak sorular öğrencilerin bağımsız düşünme ortamını zedelememelidir. Şu sorular kullanılabilir.

(1) Bu problemde neyin bulunması isteniyor?

(2) Hangi bilgiler verilmiştir? Neyi biliyorsun, hatırla.

(3) Buna benzer, daha önce başka bir problem çözdün mü? Orada ne yaptın, hatırla?

(4) Bu problemi çözemiyorsan, buna benzer daha basit bir problem ifade edip çözebilir misin?

(5) Tasarladığın çözümde bütün bilgileri kullanabiliyor musun?

(6) Bu problemin cevabını tahmin edebiliyor musun? Hangi değerler arasındadır?

Buradaki soruların problemin anlaşılmasıyla çok yakından ilişkili olduğu açıktır. Çünkü uygun stratejinin seçilmesi, problemi anlamaya ve stratejileri tanımaya bağlıdır. Bir problemin çözümünde bazen bir, bazen birkaç strateji birlikte kullanılır. Bazen de aynı bir problemin çözümüne farklı stratejiler uygun düşebilir. Bu stratejilerin başlıcaları şunlardır:

1) Sistematik Liste Yapma

2) Tahmin ve Kontrol

3) Diyagram Çizme

4) Bağıntı Bulma (Veriler arasında ilişki arama)

5) Eşitlik Yazma

6) Tahmin Etme

7) Benzer Basit Problemlerin Çözümünden Faydalanma

8) Geriye Doğru Çalışma

9) Elemine Etme

10) Tablo Yapma

11) Muhakeme Etme

3) Stratejinin Uygulanması

Bu aşamada seçilen strateji kullanılarak problem çözülmeye çalışılır. Çözülmez ise problemin bir veya ikinci adımına, anlamada bir eksik olup olmadığına bakılır. Yine çözülmez ise strateji değiştirilir. Gerekli aritmetik işlemlerin yapılması da bu safhada yer alır.

4. Çözümün Değerlendirilmesi

Bu son aşamada elde edilen sonuçların doğru ve anlamlı olup olmadığına bakılır. Bunun için elde edilen sonuç tahmin edilenle karşılaştırılır veya işlemlerin sağlamaları yapılır. Sonuçların anlamlı olup olmadığı ise çıkan cevabın gerçek hayata uygunluğunun kontrol edilmesiyle anlaşılır. Benzer bir problemle karşılaşılırsa onun nasıl çözüleceği tartışılır. Başka bir çözüm yolunun olup olmadığı araştırılır. Kullanılan stratejinin neden seçildiği açıklanır.

Problemin çözümüne uygun bir başka strateji var ise, bu stratejilerden hangisinin daha iyi olduğu tartışılır. Problemdeki verilenler ve istenenler değiştirilerek, böyle durumlarda elde edilen problemin nasıl çözüleceği üzerinde durulur. Bu basamaktaki etkinlikler; o problemi çözmekten daha çok genel anlamda problem çözme gücünü geliştirmeye yöneliktir.

Dört işlem problemlerinin çözümleri, bu dört basamağın esaslı bir uygulaması olmayıp daha çok, onların uygulanmasında gerekli olan temel becerilerin kazandırılmasıyla ilgilidirler. Çocuklar ilkokul yıllarında bu rutin problemlerle daha çok meşgul edilmeli, zaman içinde artarak gerçek problemlerle yüzyüze getirilmelidir. Bu zamanlama aşağıdaki gibi bir şema ile gösterilebilir.

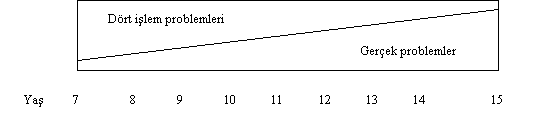
Şekil 2: İlköğretimde problem türlerinin yeralışı

Bu düşünceyle, burada problem çözme öğretimini iki ayrı başlık altında ele alınmasında yarar vardır.

Dört İşlem Problemlerinin Çözümünün Öğretimi

Dört işlem problemleri bir çözüm bekleme, öğrenilen bilginin yeniden düzenlenmesi, ne yapılacağına öğrencinin karar vermesi bakımından gerçek hayat problemlerine benzerler. Bir çeşit onların minyatürü gibidirler. Dolayısıyla çözümlerinde izlenen yol da hemen hemen aynıdır. Çocuklar ilkokula yeni başladıklarında bu tür problemlerle karşılaşır ve bunların çözümünü öğrenirken problem çözmeyle ilgili verileni isteneni yazma, şekil çizme, işlemleri yapma, sağlama yapma, sonuçları listeleme, benzer problemler yazma gibi temel becerileri kazanırlar.

Bazı matematik kitapları hatalı bir tutumla sadece tek doğru cevabı olan dört işlem problemleri içerirler. Konular arasındaki ilişkileri, problemlerin karşılaşılabilen çeşitliliğini, yorumlama ve uygulamayı gözardı edip sadece işlem becerilerini geliştirmeyi amaçlarlar.

Gerçek hayatla pek ilgileri yoktur. Bu bakımdan ders kitapları hazırlanırken veya ders hazırlıkları yapılırken tek doğru cevabı olan soruların yanısıra aşağıdaki tür sorulara da yer verilmesi gerekir.

* Çözümsüz (çözümü olmayan),

* Birden çok çözümü olan,

* Eksik ya da fazla bilgi içeren,

* Bir formülün uygulanmasını gerektiren,

* Sayısal veri içermeyen,

* Şekil ya da çizim yapmayı gerektiren,

* Gerçek hayatın bir uygulamasını konu edinen,

* Veri toplamayı ve ders dışında araştırma yapmayı gerektiren,

* Tablo ve grafiklerin yorumunu gerektiren problemlere yer verilmelidir.

Ayrıca bir problemin çözümünün arkasından verilerin değişmesi hâlinde çözümün nasıl olacağı öğrencilerle tartışılmalıdır(5).

Öğrencilerin gerek zihinden gerek yazılı problem çözmede ihtiyaç duydukları en temel beceri işlem yapmadır. Yazılı işlem yapma, sayı sisteminin ve basamak kavramının, zihinden işlem yapma ise işlem kolaylıklarının iyi bilinmesine bağlıdır. İşlem kolaylıklarının herbiri işlemlerin özelliklerinin bir sonucu olup, çoğu öğrenci bu özellikleri bilmese de, işlem kolaylıklarını sezgisel olarak kavrayabilir. Özellikle ilköğretimin ilk yıllarında problem çözmede zihinden işlem yapmaya sık başvurulur. Zihinden işlem yapmada sayıların 10 ile ilişkileri önemlidir ve bunun kavranması, öğrencilerde zihinden işlem yapmanın eğilimini artırır. Zihinden problem çözmenin en etkili araçlarından biri boş sayı doğrusudur. Aşağıda “48 sayfa olan bir hikayenin 26 sayfasını okudum. Okuyacak kaç sayfa daha var?” probleminin zihinden çözümünde boş sayı doğrusunun kullanımına iki örnek verilmiştir.

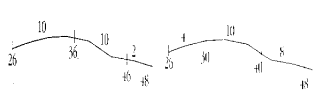
Şekil 3: Zihinden problem çözmede boş sayı doğrusunun kullanımı

Özetle zihinden işlem yapma ve problem çözme, kağıt kalem kullanmadan işlem yapmanın ötesinde birşeydir ve bir tekniği vardır.

İlköğretim Matematik Programı (s.28), çocukların iyi bir problem çözücü olması için, problem çözerken aşağıdaki adımlara uymalarının uygun olacağını ve bu davranışlardaki eksikliklerin giderilmesi gerektiğini belirtmiştir.

Bunlar sırasıyla aşağıdaki gibidir.

1- Problemde verilen ve istenenleri söyleme, yazma,

2- Problemi özet olarak yazma,

3- Probleme uygun şema ya da şekil çizme,

4- Problemin çözümünde başvuracak işlem ya da işlemleri sebepleri ile birlikte sırasıyla söyleme yazma,

5- İşlem sonuçlarını ve problemin sonucunu tahmin edip söyleme yazma,

6-İşlemleri yapma, sonucu söyleme, yazma

7-Problemin çözümünün doğru yapılıp yapılmadığını, yanlış yapılmış ise yanlışını belirterek söyleme yazma,

8-Problemin çözümünü, varsa değişik yolla yapma ve sonucu söyleme yazma,

9- Öğrenilen bilgileri kullanabilecek şekilde bir problem söyleme yazma,

Bu davranışlar dört işlem problemleriyle ilgilidir ve yukarıda verilen genel açıklamalarla birlikte ele alınması halinde problem çözme öğretiminin daha etkili olması beklenir.

Gerçek Hayat Problemlerinin Çözümlerinin Öğretimi

Bu tür problemler hayatta karşılaşılan veya karşılaşma olasılığı bulunan problemlerdir. Bunların çözümleri Polya’nın verdiği dört aşamanın tam bir uygulamasıdır. İlköğretimde çocukların yaş ve sınıf düzeylerine göre bu tür problemlerle karşılaştırılmaları onların problem çözmeden beklenen amaçlara ulaşmasına önemli katkılar sağlar, bağımsız düşünebilme güçlerini ve yaratıcılıklarını geliştirir. Problemlerin üzerinde, 3-4 kişilik gruplar halinde birlikte düşünülmesi ve tartışılması düşüncenin devinimi ve öğrencilerin birbirlerinin eksiklerini gidermeleri bakımından önemlidir.

Aşağıda gerçek hayat problemlerinin çözümlerinde kullanılan stratejilerin herbirinin öğretiminin açıklanmasının bu yazının kapsamını genişleteceği düşüncesiyle sadece iki örnek verilmiştir.

(1) Sistematik Liste Yapma Stratejisi

Bazı problemlerin çözümü bir işle ilgili mümkün olan bütün hallerin bilinmesini gerektirir. Böyle durumlarda çözüme ulaşmak için verilerin veya bulguların, dikkatli seçilmiş bir yöntemle listesini yapmak gerekir.

Aşağıda bu strateji ve bu stratejinin sınıf içinde nasıl öğretileceğini gösteren bir etkinlik sunulmaktadır.

Etkinlik: Sistematik liste yapma stratejisini tanıma ve problem çözmede kullanma.

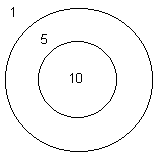
Grup: 3-4 kişi

Problem: “Şekildeki atış tahtasına üç atış yapan bir kimse kaç değişik toplam puandan birini almış olur?” probleminin grupta çözülmesi, sonra çözümün aşağıdaki çözümle karşılaştırılması.

* Problemin anlaşılması

Atış levhasındaki puanlar biliniyor. Bir kişi arka arkaya 5,5,5 veya 10,5,1 vs. gibi bir puan serisi elde edecektir. Problemde kaç değişik toplam puandan birisinin alınmış olduğu istenmektedir.

* Stratejinin seçimi ve kullanımı: Liste yapma. Atış yapan en az 3 (1+1+1), en çok 30 (10+10+10) puan alır. Yapılacak liste bu aralıkta alınabilecek tüm puanları göstermelidir. Liste yapmada üçü de aynı olan, sonra ikisi aynı olan, daha sonra üçü de farklı olan atışlar şeklinde bir sıra izlenebilir. Aşağıdaki çözümde bu yaklaşım ile bir liste yapılmıştır.

Atış	Atış	Atış	Toplam Puan
10	10	10	30
5	5	5	15
1	1	1	3
10	10	5	25
10	10	1	21
5	5	10	20
5	5	1	11
1	1	10	12
1	1	5	7
10	5	1	16

* Çözümün değerlendirilmesi:

Böyle bir problemin çözümünde en önemli nokta sıralamaya nereden başlanacağını iyi kestirmektir.

Eğer dördüncü bir puan söz konusu olsaydı kaç satırlı bir liste oluşurdu?

Bu problemi çözmeseydiniz, iki puan içeren bir benzer problemden yararlanabilirmiydiniz? Böyle bir problem yazınız? sorularının tartışılması.

(2) Diyagram Çizme Stratejisi

Bir problemle ilgili olarak verilerin arasındaki ilişkileri gösteren temsili şemaya diyagram denir. Diyagram çizme çözümü görmeyi kolaylaştırır. Aşağıda bu strateji ve bu stratejinin sınıf içinde nasıl öğretileceğini gösteren bir etkinlik verilmiştir.

Etkinlik: Diyagram çizme stratejisini tanıma ve problem çözmede kullanma.

Grup: 3-4 kişi

Problem: “Bir pasta 5 bıçak hareketi ile en çok kaç parçaya ayrılır?” probleminin grupta çözülmesi ve çözümün aşağıdaki çözümle karşılaştırılması.

* Problemin anlaşılması:

Bir pasta 5 bıçak hareketiyle kesilecek. Parçaların aynı büyüklükte olması söz konusu değil. En çok kaç parça elde edilebileceği sorulmaktadır.

* Stratejinin seçimi ve kullanımı: Diyagram çizme. Bir pasta şeması ve bir, iki bıçak kesimi ile elde edilen parça sayılarının bulunması çözümü kolaylaştırır. Parça sayısının en çok olabilmesi için her kesimin diğerlerini kesmesi gerekir.

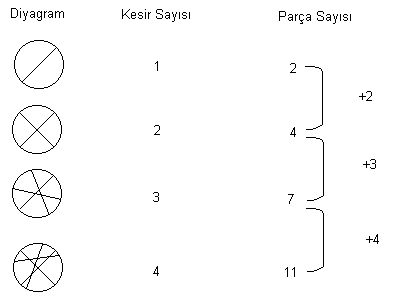
Yukarıdaki tabloda bıçak kesim sayılarının artmasına bağlı olarak parça sayılarının her seferinde bir önceki artışa göre 1 daha fazla arttığı gözlenmektedir. 5. kesim ile en fazla 15+5=16 parça elde edilecektir.

* Çözümün değerlendirilmesi

Bu problemde kesim sayısı 5 yerine 10 veya daha fazla olsa, parça sayıları arasındaki yukarıdaki ilişki görülebildiği takdirde çözüm kolaydır. Kesrin sayısının en çok olması aynı noktadan ikiden çok kesimin geçmemesi ile elde edilmektedir.

Not: Bu problemde birkaç strateji birlikte kullanılmıştır. Diyagram çizme yanında parça sayıları arasındaki ilişki görüldüğü ve bundan yararlanıldığı için bağıntı bulma, 5 bıçak yerine, 1,2 ve 3 bıçak kesimleri ile ilgili problemler çözüldüğü için küçük örneklerden yararlanma stratejileri kullanılmıştır. Yani bu çözüm üç stratejinin kullanımına örnek oluşturmaktadır (6).

SONUÇ VE ÖNERİLER

İlköğretimde problem çözme ile ilgili çalışmaların dört işlem problemlerinin yanısıra gerçek hayat problemlerini konu edinmesi, batı ülkelerinde de çok eski değildir. Bu çalışmalar son 20-30 yılın çalışmalarıdır ve bu konudaki literatür oldukça gelişmiştir. Artık gelişmiş ülkelerde matematik öğretiminin odak noktası problem çözme öğretimidir ve problem çözme öğretimi dört işlem problemlerinin yanısıra veri analizi, çözüm stratejilerini tanıma ve kullanma, araştırma yapma, grupla çalışma etkinliklerini de içeren gerçek hayat problemlerinin çözümüne çokça yer vermektedir. Tahminde bulunma, veri toplama, ölçme ve hesaplama becerileri gibi problem çözmeye katkı veren çalışmalar önemsenmektedir.

Matematik evrensel olduğu için öğretimi de evrenseldir. Bu yüzden, ülkemizde problem çözme öğretiminin bu çalışmada önerilen biçimiyle uygulanmasında herhangi bir güçlük söz konusu değildir. Türkiye’de öğretmen yetiştirme programları ilköğretim öğretmenleri bu çalışmaları tanıma ve uygulamaya, daha fazla geç kalmadan geçmeli, deneysel araştırmalarla her sınıf ve yaş düzeyine uygun problem çözme yaklaşımları ortaya konmalı ve öğretim programları buna göre yeniden gözden geçirilmelidir.

(*) Uludağ Üniversitesi, Eğitim Fakültesi, İlköğretim Bölümü.

(1)Heddens JamesW. adl William R.Speer, Today’s Mathematics Merril Publishing Co. 1997.

(2) Van De Walle John A., Elementary School Mathematics, Virginia Commenralth Universitl, Longman, 1994.

(3)Souviney,Randall J., Learning to Teach Mathematichs, Merril Publishing Company, 1989, s.66.

(4)Kennedy Leonard M. and StevenTipps, Guiding Children’s Learning of Mathematics Wadsworth pb. Co, Belmount, CA; 1991, s.126.

(5)Billstein Rich and Sholomo Libeskind, Johny W. Loft, A Problem Solving Approaht to Mathematics ForElementary School Teachers, The Benjamin Cummings Publishing Company. Inc. 1990.

(6)Murat Altun, Matematik Öğretimi,Alfa Yayıncılık, 1997, s.135.