İlköğretimde Niçin ve Nasıl Bir Geometri Öğretimi |
M. Hikmet DEVELİ* |
||||||||||||||||||||||||||||||||||||||
|
Giriş Geometri, dar sözlük anlamı ile yer ölçüsü demektir. Ansiklopedik anlamı oldukça geniştir. Geometri, bir kavramlar kümesi olarak ele alındığında; tanımının giderek genişlediği ve durmadan genişleyeceği görülür. Matematik olgusunun ilk esin kaynakları doğa ve yaşamdır. Geometri yanını doğa ile ilişkilendirmek daha kolay ve gereklidir. İnsanın geometri adına yaptığı, doğada var ve yadsınamaz gerçekleri görmek, bunlar arasındaki ilişkileri keşfederek soyut alanda (zihinde) bu ilişkileri yeni gerçek ve yeni ilişkilere götürmek olmuştur. Her çocuk, gelişim sürecinde insanlığın geometri bağlamında yaşadıklarını yaşayacaktır. Çağdaş eğitim bilimciler çocukların eğitim-öğretim sürecinde (özellikle ilköğretimde) çevreyi ve olayları eleştirel biçimde gözleyip akranları ile görüş alışverişinde bulunarak -öğretmenin düzenleme ve yol gösterme dışında öğrenci adına hiçbir ek eylemde bulunmadığı ortamlarda- bilgi kazanması gerektiğini savunmaktadırlar. Bu eğitim-öğretim türüne matematik dili ile Realistik Eğitim (gerçekçi eğitim) denmektedir (1, 2). Bu yüzden; çocuğun geometri adına yapacağı tüm zihinsel ve bedensel etkinlikler, kavram ve bilgileri ilk defa kendisi bulmuş ve kazanmış duygusu içinde gerçekleşmelidir. Eğitimcilere düşen görev ise; çocuğa bu zorlu yolda özgür düşünce ortamları hazırlamak, eğitim-öğretim adına kazanılmış her türlü olanağı onun hizmetine sunmaktır. Aksi hâlde, yani çocuğun özgürce düşünmesine olanak bırakmadan ona aktarılacak her bilgi, görüş ve düşünce onun kendi adına düşünme yeteneğini ve isteğini azaltacaktır. Matematik öğrenme ortamlarının (özellikle geometri çalışmalarının) bu tür eğitim-öğretimin en çok verim alınan ortamları olduğu gerçeği ne yazık ki geç fark edilmiştir. Ülkemizde ancak 1990lı yılların başlarında gerçekçi eğitim modeline geçilmesi kararı alınmış ve bu amaçla Millî Eğitimi Geliştirme Projesi adı altında ciddî bir proje başlatılmıştır. Bu proje kapsamında Amerika Birleşik Devletlerinin Florida eyaletinin bir kısım ilköğretim okulları ve öğretmen yetiştiren kurumlarında yapılan bir incelemede yaparak-yaşayarak geometri öğretimi modeline uygun eğitim-öğretime Amerikada da ciddî anlamda son 25-30 yılda geçildiği, üstelik bu süreçten önceleri okul kitaplarında geometri bilgilerine çok az yer verildiği gerçeği gözlenmiştir (3). Amerikada yayınlanan eğitim araştırma yayınlarına, ülke standartlarının içeriğine ve kronolojik gelişimine bakıldığında bu gerçek açıkça görülebilir. Ancak geçen bu kısa süreç içerisinde Amerikada özellikle geometri öğretimi üzerine hızlı bir gelişim ve değişim kaydedildiği gözlenmektedir (4, 5). Bu çalışmada, çağdaş geometri öğretimi anlayışının nasıl olması gerektiği üzerinde durulmuş ve buna uygun iki etkinlik örneği sunulmuştur. İlköğretim İçin Geometri Nedir? Öğretiminin Amaçları Nelerdir? İlköğretimde geometri öğretiminin Van Hiele Geldofun verdiği geometrik düşünce düzeylerinden ilk üç düzeyi yani Tanıma (Düzey 0), İnceleme, gözlem (Düzey 1) ve İnformal Çıkarım veya Soyutlama (Düzey 2) düzeylerini kapsaması gerektiği hemen hemen tüm eğitim-öğretim çevrelerince kabul edilmektedir (4, 5, 6). Bu yüzden ilköğretimde geometri öğretimi Tanıma düzeyinden başlayıp Soyutlama düzeyine getirilmelidir. Bundan dolayı ilköğretim öğrencisi adına; geometri, aşağıdakilerden her biri veya hepsinin birleşimidir diyebiliriz (7, 8). Günlük yaşamda gördüğü şekil ve cisimlerin kümesi Şekil ve cisimlerin bulmacası Nokta ve çizgiler oyunu Çevreyi tanıma ve değerlendirme aracı Sanatsal ve mimarî yapıların, aygıtların çizgilerle yorumu Model inceleme, tasarlama ve oluşturma işi. İlk eleştirel geometrik gözlemlerin yapıldığı, sezgilerin oluştuğu, kavram ve bilgilerin kazanıldığı dönem olan ilköğretimde geometri öğretiminin önemi sonraki dönemlere oranla daha büyüktür. Ancak öğretim sistemimizde geometri öğretimine matematiğin diğer alanlarından daha az yer verildiği ve öğretiminin genellikle tanımlar yardımı ile yapıldığı bir gerçektir. İlköğretimde geometri öğretiminin aşağıda verilen amaçları; onun önemini, önceliğini ve gerekliliğini açıkça ortaya koymaktadır. Geometri, çocuğun çevresini daha gerçekçi biçimde tanıyıp değerlendirmesini ve analiz etmesini kolaylaştırır. (Doğadaki varlıkları, oluşumları, sanatsal, mimarî ve teknolojik ürünleri vb.) Geometri, matematiğin diğer alanları başta olmak üzere; birçok bilim dalında bilgi ve beceri kazanmanın vazgeçilmez aracıdır. (Sayı, kesir, ölçü kavramlarının oluşumu, yön ve konum kavramları, madde-hareket ilişkileri vb.) Geometri, problem çözme stratejilerinin önemli bir aracıdır. (Çözüm modeli oluşturma, tasarım yapma, şemalandırma vb.) Geometri birçok meslek elemanının yardımcısıdır. (Mimar, desinatör, haritacı vb.) Geometri zihinsel gelişimin önemli bir aracıdır. (Önerme oluşturma, önerme doğrulama vb.) Geometri öğretimi erken yaşlarda oyun şeklinde başlayıp, bulmaca niteliğinde sürdürülüp, sağlam sezgi, kavram ve bilgiler kümesi olarak geliştiğinde matematiğin en ilginç ve zevkli bölümünü oluşturur. Böylece matematiğe karşı olumlu tutum geliştirme fırsatı doğurur. Etkinliklerle (Aktivitelerle) Geometri Öğretimi İlköğretimde geometri öğretimi gözlem ve sezgiye dayalı olacağına göre görsel ve somut etkinlikleri yine aynı oranda ağırlıklı olmalıdır. Özellikle nokta, doğru, düzlem, uzay ve küme gibi geometrinin tanısız temel ögelerinin kavratılmasında sezgiler önemlidir. Bu kavramların öğretimi ile ilgili etkinliklerin çevre kaynaklı olması gerekir. Etkinlikler düzenlenirken grup içinde etkileşime önem verilmeli, etki ve sonuçları önceden iyi bilinmelidir. Ayrıca etkinlikler öngörülen öğrenme ve düşünce düzeylerine uygun olmalıdır. Bu nedenle matematiğin diğer alanlarında olduğu gibi geometri etkinliklerinin düzenleme ve uygulama sürecinde aşağıdaki sorulara cevap aranmalıdır (9). I. Etkinliğin amacı nedir? 1. Etkinlik hangi yeterlikleri, istendik davranışları kazandırmaya yöneliktir? 2. Bu etkinlik için ön yeterlikler nelerdir? 3. Bu etkinliğe amacını (amaçlarını) çağrıştıracak biçimde, nasıl bir ad verebiliriz? II. Etkinlik hangi hazırlıkları gerektiriyor? 1. Etkinlik grupla mı, kişisel mi gerçekleşmeli? Grupla ise kaç kişilik gruplar? 2. Süre en az ne kadar olmalıdır? (Gerekirse etkinlik önceden öğretmen tarafından yapılmalı ve sadece süre alt limiti belirlenmelidir) 3. Gerekli araç gereçler nelerdir, nasıl elde edilebilir? III. Etkinlik nasıl gerçekleşecek? 1. Etkinlik nasıl sunulacak? (Sunuş, güdüleme, istekli kılma vb.) 2. Etkinlik sürecinde öğrenciler neleri, hangi sırada yapacaklar? 3. Öğrencilerin çalışma süresi içinde öğretmen neleri yapacak? (Denetim, yol gösterme, izlettirme, ilginç sonuçları not etme vb.) IV. Etkinlik nasıl değerlendirilecek? 1. Kişi veya grupların görüşleri nasıl alınacak? (Sözlü, yazılı, gösterimli vb.) 2. Neler tartışılacak, eleştirilecek? (Özellikle olası ilginç sonuçlar) 3. Kazanımlar neler oldu? Etkinlik amacına ulaştı mı? Tekrarlanmalı mı, benzerlerini yapmak gerekli mi? V. Geliştirme (Zenginleştirme) ve güçlendirme yapmalı mıyız? 1. Bu etkinlik geliştirilmeli mi? Niçin? Nasıl? (Ek çıkarımlar vb.) 2. Etkinlik problem çalışması ile desteklenebilir mi? (Uygulama, transfer vb.) 3. Örnek çalışmalar sergilenecek mi? 4. Ödev etkinlik verilebilir mi? Yukarıdaki sorular demetine bir Etkinlik Yönergesi de diyebiliriz. Bu yönergeye uygun biçimde hazırlanan her etkinlik aynı düzende bir Etkinlik plânı gerektirir. Etkinlik süresi bir eğitim-öğretim oturumunun tümünü kapsıyor ise etkinlik plânı, Ders Plânı şeklinde olmalıdır. Eğer etkinliğimiz bir ders oturumunun bir bölümünü oluşturuyor ise etkinlik plânının amaçlar ve değerlendirme kısımları ders plânının bütünü içinde ilgili yeri alacaktır. Geri kalan kısımları ise ders plânının Geliştirme Bölümünün bir parçası olacaktır. Etkinlik Örnekleri Bu bölümde verilecek olan etkinlik örneklerinden ilki bir önceki bölümde sunulan Etkinlik Yönergesinin tüm ayrıntılarını içerecek şekilde hazırlanmıştır. İkincisi ise ilköğretimde geometri öğretiminin eğlenceli bir uğraş olarak sunulabileceğini örneklemek amacı ile hazırlanmış olup hazırlanış ve uygulanışı ile ilgili ayrıntılara girilmemiştir. ETKİNLİK I: Üçgen türleri (Üçgenlerde sınıflama) Sınıf: 5 Amaçlar: 1- Üçgenleri kenarlarına göre sınıflama bilgisi 2- Üçgenleri açılarına göre sınıflama bilgisi Ön kavram, bilgi ve yeterlikler: Üçgen kavramı, üçgende kenar ve açı kavramı, açı türleri bilgisi, uzunluk ve açı ölçü birimleri. Grup çalışması: 2-4 kişilik gruplar Materyal araç ve gereç: Her grup için iki dosya kâğıdı (veya aynı büyüklükte karton), her biri en az 10 cm uzunluğunda 2-3 mm eninde çeşitli renklerde karton şeritler (var ise yassı saman çöpleri olabilir), makas, maket bıçağı, sıvı yapıştırıcı, cetvel, açı ölçer, tepegöz veya bilgisayar. Süre: En az 80 dakika Sunuş: Çalışmanın adı söylenir, amacı açıklanır, materyaller gruplara dağıtılır. Grupların yapacağı işler sırayla söylenir. Bu sıra şu şekilde olabilir. 1- Şeritlerden (çöplerden) 2, 3, 4, 5er cm.lik yeteri kadar parça kesilmesi (en az onar adet), 2- Elde ettikleri parçalar ile kendilerince olası tüm üçgenleri tasarlayıp kartonlar üzerinde düzenleyerek yapıştırmaları. 3- Oluşan her üçgenin kenar uzunluklarını ve iç açılarını ölçüp buldukları değerleri ilgili yerlere yazmaları. 4- Düzenledikleri her bir üçgene kenar uzunluklarına ve açı ölçülerine bakarak önce kenarlarına sonra açılarına göre kendilerince birer ad vermeleri ve bu adı üçgenin altına yazmaları. 5- Elde ettikleri sonuçları sınıfa -gerektiğinde- sunmaları. Gerçekleştirme: Gruplar öngörülen işleri yapmaya başlarlar. Bu süreç etkinliğin en çok zaman alan kısmıdır. Öğrenciler çalışırken öğretmen bu etkinlik için öngörülen aşağıdaki denetleme, yol gösterme, uyarma ve gözlem işlerini yapar. 1- Şeritlerin istenen uzunlukta kesilmesi. 2- Üçgenlerin köşelerinin düzgün biçimde oluşturulması. 3- Ölçülerin doğruluğu, çizelgede ilgili yerlere yazılımı. 4- Üçgenlerin farklılığı (değişik üçgenler). 5- Olası ilginç sonuçlar (yanlış ve yetersiz çalışmalar, oluşmayan üçgenler vb.). 6- Grup içi etkileşim (tartışma, görüş alışverişi vb.). Değerlendirme: Grupların elde ettikleri sonuçları sınıfa sunmaları isteneceği gibi, öğretmen aşağıdaki soruları sınıfa yönelterek bu sorulara her gruptan veya birkaç gruptan cevap isteyebilir (ilginç sonuçlara ulaşan gruplara öncelikle söz vermelidir). 1- Kaç tane üçgen düzenleyebildiniz? 2- Size göre kaç farklı üçgen türü var? (Veya kaç farklı ad verebildiniz?) 3- Üç kenarı da farklı kaç üçgen yaptınız? 4- İki kenarı eşit kaç üçgen yaptınız? 5- Üç kenarı da eşit kaç üçgen yaptınız? 6- Açılar için benzer soruların sorulması. 7- Kenarları 2 cm, 3 cm, 5 cm üçgen yapan grup var mı? 8- Dar, dik ve geniş açılı üçgenleri belirlediniz mi? Yukarıdaki soruların (ve benzeri soruların) uygun cevapları çoğaldıkça öğretmenin hakemliğinde üçgenlerin kenarlarına ve açılarına göre iki tür sınıflaması sınıfça doğru biçimde elde edilecektir. Örnek çalışmalar sınıfın uygun bir yerinde sergilenebilir. Not: 1. Eğer yeter sayıda bilgisayar (ve uygun program) var ise bu etkinliğin gerçekleştirme bölümü gruplarca (veya kişisel olarak) bilgisayarda yürütülebilir. Bu durumda materyaller de değişecektir. 2. Öğretmen etkinliğin Sunuş kısmında üçgenlerin kenarlarına göre; çeşitkenar, ikizkenar, eşkenar ve açılarına göre; dar açılı, dik açılı ve geniş açılı şeklinde iki sınıflamasının varlığından öğrencileri önceden haberdar edip bu sınıflamaya uyan örnekleri üretmelerini isteyerek etkinliği amacına ulaştırabilir. Ancak öğrenciye düşünmesi ve kendisinin bulması gibi fırsatları veren ve yukarıda örneklenen şeklin daha yararlı olacağı kanısındayız. Genişletme (Zenginleştirme): a) Ek Çıkarımlar: Aynı ders oturumunda veya bir sonraki oturumda yukarıdaki etkinlik, sınıflamanın düzenli bir çizelgeye aktarılması ve ayrıca üçgende kenar-açı ilişkisini görme amacına yönelik olarak aşağıdaki gibi genişletilebilir. Öğretmen gruplarının sonuçlarını sınıfça belirlenen sınıflamayı da göz önüne alarak -örnek bir satırı öğretmen tarafından doldurulmuş- aşağıdaki çizelgeye işlemelerini ister. Daha sonra doldurulan çizelgeler üzerinde tartışma açılıp gereksiz satırlar (yanlış, tekrar eden, benzer vb.) silinerek çizelgeler istenilen şeklini alır.
Bu çizelge üzerinde açı-kenar veya kenar-kenar ilişkisini ortaya çıkarmak için aşağıdaki (veya benzeri) sorular sorularak tartışma açılabilir. 1- Kenar uzunlukları 2, 3, 4 cm olan üçgeni neden yapamadık? 2- Üçgenlerde iki kenarın toplamını (ve farkını) üçüncü ile karşılaştırınız. Ne gördünüz? 3- Üçgenlerinizde kenarların karşısındaki açılara bakınız. En uzun kenar karşısında nasıl bir açı var? 4- Kenar uzunlukları 3, 4, 5 cm olan üçgeninize dikkat ediniz. Nasıl bir üçgen, neden? 5- Çeşitkenar, ikizkenar ve eşkenar üçgenlerinize bakınız. Açıları arasında ne gibi ilişkiler var? Buradan; kenar uzunluklarına bakarak açılar hakkında neler söyleyebiliriz? 6- Üçgenlerin açılarına göre yeni bir sınıflamasını yapabilir misiniz? Nasıl? 7- Açıların toplamına dikkat ettiniz mi? Ne olmalıydı? b) Problem ile güçlendirme: Bu etkinlik ile amaçlanan davranışları
güçlendirmeye yönelik çok sayıda problemden bir tanesi aşağıdaki şekilde
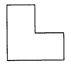
olabilir. Problem: Yandaki dikdörtgen iki doğru parçası ile eşit iki dik üçgen ve bir ikizkenar üçgene bölünmüştür. Siz de kısa kenarlarının dördü de eşit olan aşağıdaki şekli üç doğru parçası ile eşit iki dik üçgen ve eşit iki geniş açılı üçgene bölünüz.
c) Ödevlendirme: Yukarıdaki çizelgenin tamamlanması, kenar-açı ilişkilerinin görülmesi veya örnek problemin benzerleri ödev etkinlik olarak verilebilir. Etkinliklerin kavram bilgisi ile ilgili olanlarına bir örnek yukarıda verildi. Kazanılan bilgilerin pekiştirilmesi için de değişik etkinlikler düzenlenebilir. Aşağıda böyle bir etkinlik verilmiştir. ETKİNLİK II: Şekillerin özellikleri Buraya iki basamaklı bir sayı yazınız : . . . İkizkenar üçgenin simetri doğrusu sayısını ekleyiniz : . . . Dik üçgeninin dar açı sayısı ile çarpınız : . . . Üçgenin köşegen sayısını çıkartınız : . . . Yamuğun parelel kenarlarının sayısına bölünüz : . . . Ekşenar üçgenin simetri doğrusu sayısını ekleyiniz : . . . Dikdörtgeninin eşit açı sayısı ile çarpınız : . . . Eşkenar üçgenin eşit açı sayısının iki katını çıkartınız : . . . Paralel kenarın simetri doğrusu sayısını çıkartınız : . . . Eşkenar dörtgenin eşit açı sayısını ekleyiniz : . . . Karenin eşit kenar sayısına bölünüz : . . . İlk yazdığınız sayıyı çıkartınız : . . . Bulduğunuz sayı 3 mü? Değilse yeniden deneyiniz!.. Sonuç ve Öneriler Bu çalışmada örneklenen etkinlikleri ve benzerlerini sınıfta gerçekleştirmenin hem olanaklar ve hem de zaman açısından zor olabileceği söylenebilir. İyi bir plânlama, biraz özveri ve elde edilmesi daha kolay olan alternatif materyallerle benzeri etkinliklerin verimli bir şekilde gerçekleştirilebileceği bu çalışmayı sunanlar tarafından yaşanmış ve izlenmiştir. Asıl güçlük etkinliklerin tasarımındadır. Bu güçlüğü aşmak için öğretmenlerin hizmetine çok sayıda örnek sunmak gerekir.
|
|
||||||||||||||||||||||||||||||||||||||
|
[ yukarı ] |
|||||||||||||||||||||||||||||||||||||||